Attention as a Softened Hash Table

initial motivation:

When dealing with sequences to sequences, the original approach was to use $seq2seq$ architecture that relied on an encoder-decoder scheme with a context hidden state to link between the two, although this approach worked fairly well and solved the limitations of many-to-many $RNNs$ , it did have its own limitations .

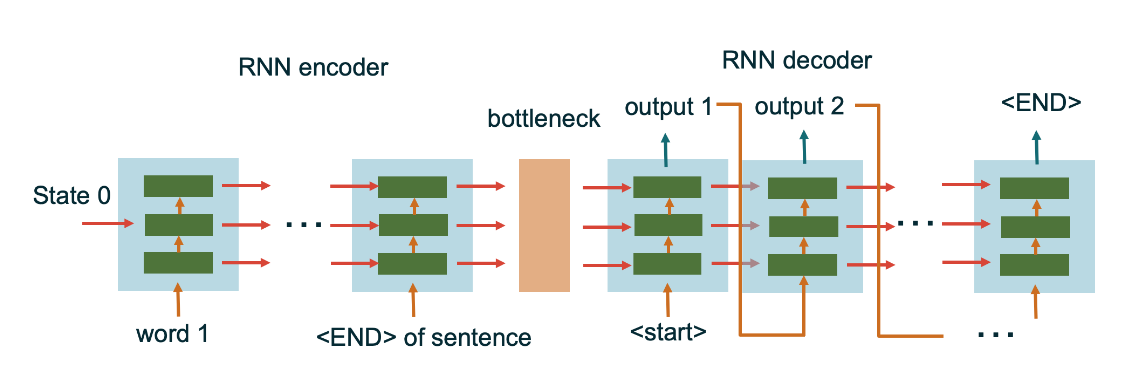
Limitations of the Encoder-Decoder architecture:

When you look at the previous encoder-decoder architecture, the first thing you might notice is that we’re squeezing all information into one context vector.
We are losing the nuance of the representation of each timestamp in the encoder.

Our encoder-decoder setup is too rigid. We're forcing a strong inductive bias by assuming all learning happens through a single context state, if only things were that simple.

What do we need?

Keep the encoder-decoder structure for efficient training.
Retain a context state to learn the full sequence representation.
Introduce a way to access different timestamps during decoding.

Ideas:

We will now try to systematically go about potential solutions until we find the best mechanism to answer our previous questions.

Idea 0:

Use a static correspondence from the encoder to the decoder, similar to the $U-Net$ architecture.

Problems:

We usually have a different length of sequences between the encoder and the decoder, this is one of the main benefits of the encoder-decoder architecture, it can naturally deal with the different sequence lengths.
We can’t know beforehand what block in the encoder corresponds to in the decoder; this is different from images where we have some sense of hierarchy that is symmetric.
Apart from the architectural considerations, the static routing itself is too limiting, this is not a problem in images due to the strong inductive bias of locality, but there's no similar constraint when talking about sequences, a block in the decoder should naturally have access to more than one state in the decoder.

Question: How to dynamically link between blocks in the encoder and those in the decoder during training time?

Idea 1:

At training time:

Allow the decoder to send a query $q$ .

Allow all previous blocks, whether inside the encoder or decoder to pick up the query and match it with a generated key $k$ .

Return the value $v$ (can be the same as the key) corresponding to the best match.

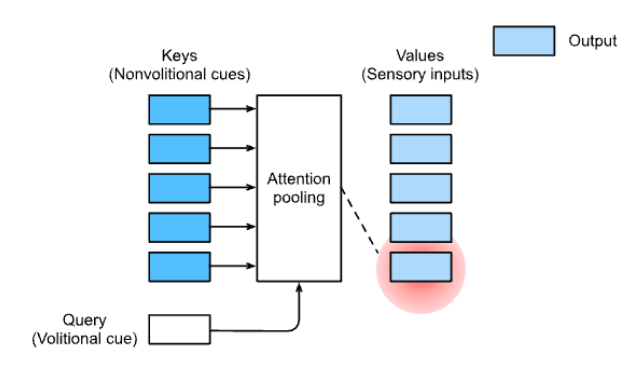
Now let's consider some design considerations with this idea.

Consideration 1:

What should the values for $q$ , $k$ and $v$ be ?

A first instinct would be to have the key and value as the hidden state at some specific layer in the previous blocks, while the query is the hidden state at this timestamp.
This is too rigid though, a better approach is to let $q$ , $k$ , $v$ be the output of some $MLP$ , which the input to, is a design choice specific to the application.
We will then, by training end-to-end find better combinations.
Think about the training dynamics and how changing these values, puts pressure on the hidden states themselves, we’re pushing the states to learn better representations based on the upstream task.

Consideration 2:

How to match between $q$ and $k$ ?

Use a hard match between $q$ and $k$

At initialization, the generation of $q$ and $k$ is random, and nothing would match, gradients are zero and nothing will change ever.
We would need to use a similarity measure between $k$ and $q$ .

Consideration 3:

What similarity function $Sim$ to use?

There are many options here, some good choices are the Inner product $q^Tk$ or radial basis function $(RBF)$ $exp(−γ∥q − k∥^2)$ .
Let suppose that $e_i = q^Tk_i$

Consideration 4:

The values of $e$ (the inner product between $q$ and $k$ ) can grow very large not due to similarity, but by the mere fact that they’re very high dimensional, this can cause problems in the stability of the Softmax specially early in training.

Let's make the following assumptions, suppose $q, k ∈ R^d$ are two random vectors with $q,k\ \sim N(\mu, σ^2I)$ , where $µ ∈ R^d$ and $σ ∈ R_+$ .

In other words, each component $q_i$ of $q$ is drawn from a normal distribution with mean $\mu$ and standard deviation $σ$ , and the same is true for $k$ .

Let's also suppose that $\mu = 0$ and $\sigma^2 = 1$ . This is justified if we suppose that $q$ and $k$ are the result of an $MLP$ initialized with Xavier/Glorot or Kaiming initialization and whose input is normalized.

These are reasonable assumptions, and at initialization we can also suppose that $q$ and $k$ are somewhat independent.

The goal now is to have similarities $e = q^Tk \sim N(0, I)$ , let's calculate the mean and variance of the similarities.

\mathbb{E}[q^T k] = \mathbb{E}[\sum_{i=1}^d q_i k_i] = \sum_{i=1}^d \mathbb{E}[q_i k_i] == \sum_{i=1}^d \mathbb{E}[q_i]\mathbb{E}[k_i] = \sum_{i=1}^d \mu_i^2 = ||\mu||_2^2

\text{Var}(q^T k) = \mathbb{E}[(q^T k)^2] - \mathbb{E}[q^T k]^2 = \mu^T \Sigma_q \mu + \mu^T \Sigma_k \mu + \text{tr}(\Sigma_q \Sigma_k) = 2\sigma^2 ||\mu||_2^2 + d * \sigma^4

Now since we supposed, $q,k\ \sim N(0, I)$ :

\mathbb{E}[q^T k] = 0 \quad \text{and} \quad \text{Var}(q^T k) =d

We can see how the variance grows as the dimension $d$ grows, luckily the solution is simple enough, we would only need to normalize $e$ by $\sqrt{d}$ to have variance of $1$ !

It's worth mentioning that the similarities can still grow during training, this is why some papers suggest applying layer normalization to the similarities before calculating the attention, you can read more at QKNorm.

Consideration 5:

How to choose from the similarity values while keeping differentiability ?

Suggestion 1: Use $arg\ max$ .

Look at the computational graph below.

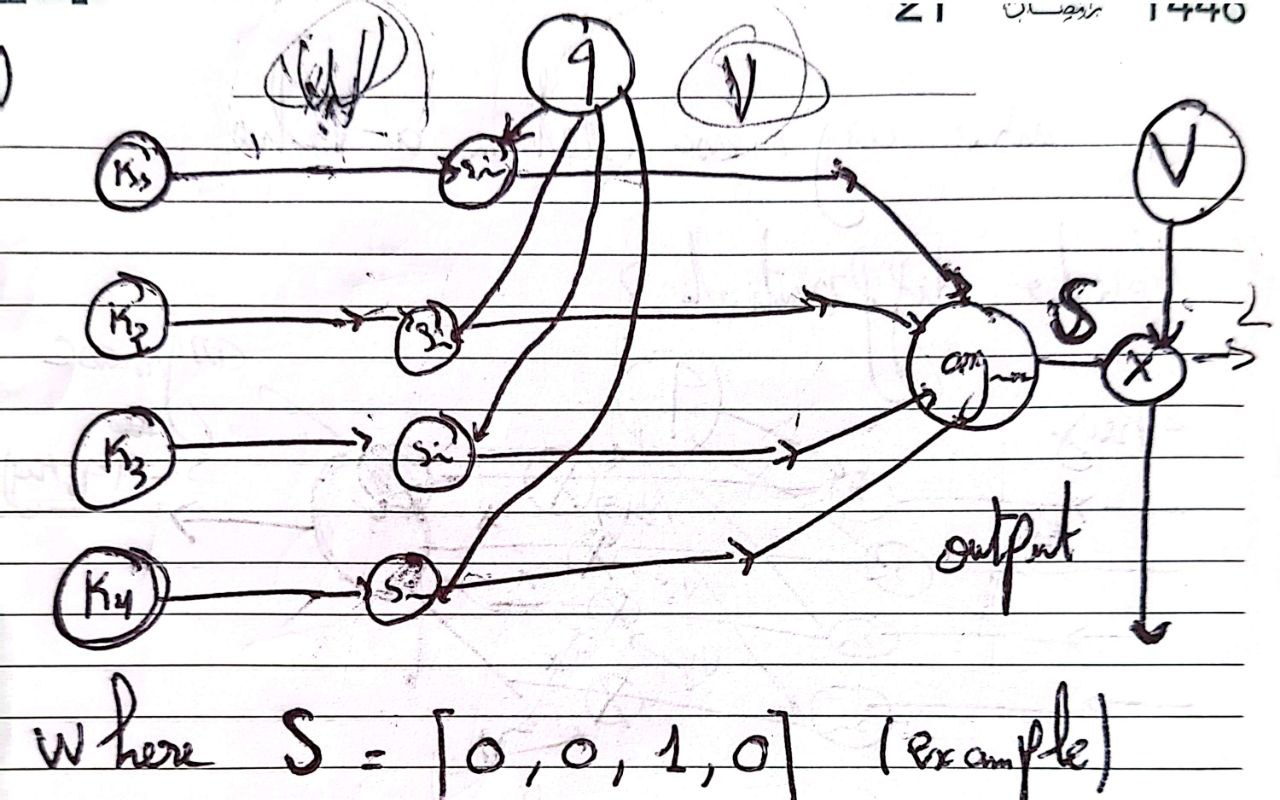
We would have gradients flowing back to the values $v$ , but since the $arg\ max$ is not differentiable (assumed to be $0$ ), keys and values will not get any updates, we will never learn a better representation than the one we got at initialization.

A philosophical way to look at this, is that changing the query slightly will not change the match, hence the zero gradients.

Suggestion 2: Use $max$ .

We would need to think of a way to select the values after preforming the $max$ that is differentiable. There's no clear way to do this.

We might think of using something like:

Output = max(sim(k_i, q)v_i)

But the values here aren’t normalized, their influence on deciding the similarities is not something we would want, even if normalized, this doesn’t make much sense.

Also, even if this does work, we get gradients on the keys and queries, but the gradient would only flow to the key with the wining path.

Even though we have gradients, we still wouldn't learn a better combination considering the properties of the $max$ function.

From 1 and 2, we can say that whenever we make a hard decision, there’s a gradient problem. We need to soften this hard decision.

Suggestion 3: Use a softened max operation.

A natural choice is the Softmax.

Say we have:

\alpha_i =\frac{exp(e_i)}{\sum_j exp(e_j)}

Where $e_i$ are the similarities we defined above.

If $e_d$ is the biggest value, the sum below would be approximately equal to $\sum_j exp(e_j) = exp(e_d)$ , so the coefficient $\alpha_d \approx 1$ and $\alpha_i \approx 1$ for $i \not{=} d$ .

Knowing the previous properties, we can use the previous coefficients to calculate a weighted average of values.

So finally we would have:

e_i = \frac{q^Tk_i}{\sqrt{d}}

\alpha_i =\frac{exp(e_i)}{\sum_j exp(e_j)}

Attention = \sum_i \alpha_iv_i

This is an illustrative figure of the attention mechanism we designed:

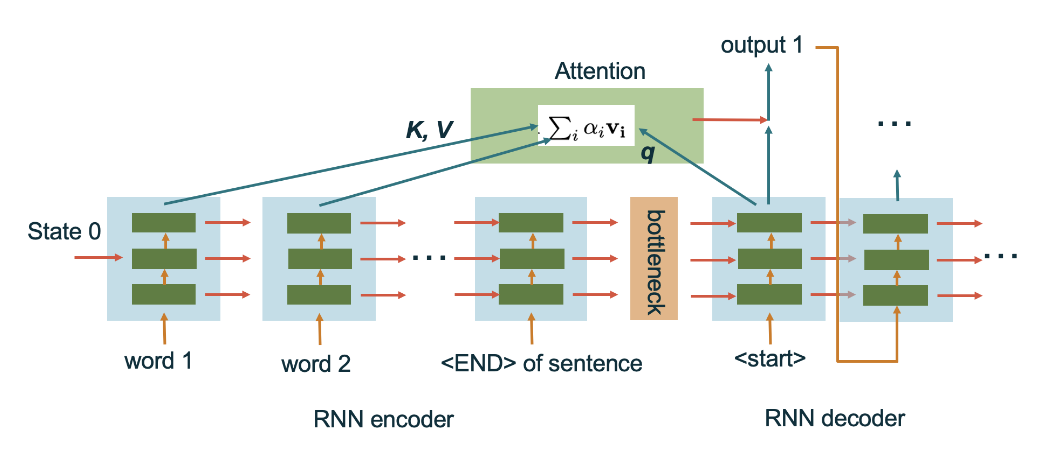
This way of understanding attention gives a strong intuition into the mechanism as we can formulate attention as a mere softened differentiable hash-table/dictionary or a quarriable softened max-pooling.

Now we presented the attention mechanism in the context of $seq2seq$ but this powerful mechanism, propped the question that changed the field as we know it, is Attention all we need ?

Acknowledgment:

This blog post was heavily inspired by UC Berekely's CS182 course by Anant Sahai.